|
Universal Programmer, EPROM Programmer |
|
Universal Programmer, EPROM Programmer |
|
Simple Explanation |
|
Faster than an 8-Gang Programmer ! 2 Major Reasons: (1) Skt 1 begins to program when skt 2 is being loaded. When skt 4 has been loaded, skt 1 is done. No waiting. |
|||
|
Device examples |
This gang programmer 

|
Conventional 8-gang 


|
|
|
27C020 PLCC, each takes 30 sec to program, 15 sec to load, 15 sec to unload |
120 sec to program 4 chips (60 sec to load, no waiting, 60 sec to unload) |
150 sec to program 4 chips (60 sec to load, wait 30 sec for programming, 60 sec unload) | |
|
240 sec to program 8 chips (120 sec to load, no waiting, 120 sec to unload) |
270 sec to program 8 chips (120 + 30 + 120=190) |
||
|
27C040 DIP, each takes 60 sec to program, 10 sec to load, 10 sec to unload |
110 sec to program 4 chips (40 sec + 30 + 40 = 110) (30 s wait is needed because loading is faster than programming time) |
140 sec to program 4 chips (40 sec load, wait 60 sec for programming, 40 sec unload=140) | |
|
190 sec to program 8 chips (80 + 30 + 80 = 190 ) |
220 sec to program 8 chips (80 + 60 + 80 = 220) |
||
|
Faster than an 8-Gang ! Reasons: (2) Conventional 8-gang programmers are inherently slower because one controller controls all sockets. If indeed it takes 30 sec to program one chip, it will take 60 seconds to program 4 chips and about 90 sec to program 8 chips. The above examples do not even take this fact into account. If it does, 8-gang programmers are much slower than the numbers shown above. |
|||
|
Mathematical Details |
|
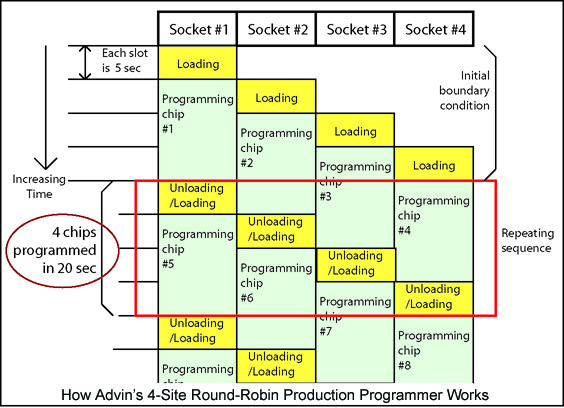
Let us take a look at a simple example (Example A): In this example, we assume it takes you 5 seconds to unload a certain programmed chip and also reload a new one into the same socket adapter. Assume that the programmer takes 15 seconds to program this type of chip. As soon as the chip is loaded into Socket #1, it will start being programmed, as shown in green below. By the time you finish loading Socket #4, chip #1 will be done and you can unload it and put in a new one at Socket #1. |
|
|
Ignoring the minor boundary conditions (starting of the batch of chips
and ending the batch), it takes 5 seconds plus 15 seconds=20 seconds
to get 4 chips programmed, as shown in the red box. That means a
throughput of (5+15)/4=5 seconds per chip.
If you are using a conventional 8-site gang programmer, you will spend 5 sec x 8=40 seconds to load the 8 chips, plus 15 seconds (could be more because the single controller needs to attend all 8 sockets) to wait for them to be programmed. The throughput in this case would be (40+15)/8=6.9 seconds per chip - 37% slower than our 4-site round-robin programmer. |
| (Time is in seconds) |
Round-Robin 4-site Programmer |
Conventional 8-site Programmer |
| Loading and unloading time per chip (L1) | 5 | 5 |
| Number of programming sites (n) | 4 | 8 |
| Total loading and unloading time for all sites (LA) | 20 | 40 |
| Time needed to program each chip (p) | 15 | 15 |
| Total time taken for n chips to be programmed (T) |
5+15=20 (L1+p) |
40+15=55 (LA+p) |
| Effective time taken to produce one chip (T/n) | 5 | 6.9 |
| Winner |
Round-Robin 4-site Programmer |
|
Round-Robin 4-site Programmer |
Conventional 8-site Programmer | |
| Loading and unloading time per chip (L1) | 5 | 5 |
| Number of programming sites (n) | 4 | 8 |
| Total loading and unloading time for all sites (LA) | 20 | 40 |
| Time needed to program each chip (p) | 30 | 30 |
| Total time taken for n chips to be programmed (T) |
5+30=35 (L1+p) |
40+30=70 (LA+p) |
| Effective time taken to produce one chip (T/n) | 8.8 | 8.8 |
| Winner | It is a tie | It is a tie |
|
Round-Robin 4-site Programmer |
Conventional 8-site Programmer | |
| Loading and unloading time per chip (L1) | 5 | 5 |
| Number of programming sites (n) | 4 | 8 |
| Total loading and unloading time for all sites (LA) | 20 | 40 |
| Time needed to program each chip (p) | 60 | 60 |
| Total time taken for n chips to be programmed (T) |
5+60=65 (L1+p) |
40+60=100 (LA+p) |
| Effective time taken to produce one chip (T/n) | 16.3 | 12.5 |
| Winner |
Conventional 8-site Programmer |
|
Conclusion 1: IF it takes you 5 seconds to unload and load a device: THEN our 4-site round-robin gang programmer beats an 8-site conventional gang programmer when the device takes less than 30 seconds to program (or erase, program and verify, whatever you need to do with the programmer in the "auto" sequence). If it takes you 10 seconds to unload and load a device, then the break-even point would be changed from 30 seconds to 60 seconds. |
|
Round-Robin 4-site Programmer |
Conventional 8-site Programmer | |
| Loading and unloading time per chip (L1) | 10 | 10 |
| Number of programming sites (n) | 4 | 8 |
| Total loading and unloading time for all sites (LA) | 40 | 80 |
| Time needed to program each chip (p) | 60 | 60 |
| Total time taken for n chips to be programmed (T) |
10+60=70 (L1+p) |
80+60=140 (LA+p) |
| Effective time taken to produce one chip (T/n) | 17.5 | 17.5 |
| Winner | It is a tie | It is a tie |
|
Conclusion 2: IF it takes you 10 seconds to unload and load a device: THEN our 4-site round-robin gang programmer beats an 8-site conventional gang programmer when the device takes less than 60 seconds to program (or whatever you need the programmer to do for you in the "auto" sequence). Conclusion in General: Our 4-site round-robin gang programmer is more favored when: A. The operator takes more time to unload and reload a device. OR: B. The devices takes less time by the programmer to get programmed. Since our 4-site round-robin gang programmers are very fast and take much less than 60 seconds to erase, program and verify most devices, they pay for themselves faster than conventional gang programmers.  See the Productive Round-Robin Gang Programmer
See the Productive Round-Robin Gang Programmer |